How to Reverse a String

Question: given a string, reverse it. You can destroy the original string or return a new string that is the reverse of the original string. For example, if input is "abcde", output will be "edcba".

Solution: this is a simple problem. We just need to traverse the input string from last character to the first character. As we traversing the input string, we add its characters to the output string. At the end of the traversal, we have an output string that is the reverse of the original. Here is the code in JavaScript:

function sReverseStr(pInputStr)
{
   if (pInputStr === null || pInputStr === undefined)
      return;

   var pResultStr = "";
   
   for (var i = pInputStr.length - 1; i > -1; i--)
   {
      pResultStr += pInputStr.charAt(i);
   }

   return pResultStr;
}

Code Explanation: the code is straight forward. Here is the breakdown:

• First, we check for invalid input. Nothing new here.
• Next, we allocate a new string named pResultStr.
• The for loop goes through each character in the input one by one from the end to the beginning. Then we add each of those character to the new string.
• When the for loop finishes, pResultStr is now the reverse of the input. We simply return it.

That's all for this post. Thanks for reading :)

Minimum Distance Between Two Elements in an Array

Question: given an array and two elements, find the minimum distance between the elements in the array. The array may have duplicates. For example, if the array is (2, 1, 3, 4, 0, 2, 5) and the two elements are 4 and 5, then the min distance is 3 because 4 is at index 3 and 5 is at index 6.

Solution: this problem can be solved using two index trackers. The idea is to loop through the array and keep track of the indices of elements that have the same values with the inputs. At the same time, calculate the distance between those two indices and keep the smallest distance.

This solution works great because it doesn't compare all possible distances of inputs when there are duplicates in the array. A naive solution would be computing all different distances between elements that have the same values with the inputs and then return the smallest distance. Here is the implementation in JavaScript:

function nMinDistanceBetweenTwoElements (nInputArray, nNum1, nNum2)
{
   if (nInputArray.length <= 0)
   {
      document.write("Empty Array!");
      return -1;
   }

   var nPos1 = nPos2 = nDis = nInputArray.length;

   for (var i = 0; i < nInputArray.length; i++)
   {
      if (nInputArray[i] == nNum1)
         nPos1 = i;
      else if (nInputArray[i] == nNum2)
         nPos2 = i;

      if (nPos1 < nInputArray.length && nPos2 < nInputArray.length)
      {
         if (nDis > Math.abs(nPos1 - nPos2))
            nDis = Math.abs(nPos1 - nPos2);
      }
   }

   return nDis == nInputArray.length ? -1 : nDis;
}

Code explanation: the method accepts three parameters. nInputArray is an array of integers. nNum1 and nNum2 are the two numbers that we must find the minimum distance between them. Here are the steps in the method:

1. First, we check for the length of the array. If the client passes in an empty or invalid array, we return -1 and an error message.
2. Next, we declare three variables. nPos1 and nPos2 keep track of the indices of the first number nNum1 and the second number nNum2 respectively. nDis keeps track of the minimum distance between the two numbers. We also initialize all of these variables to the input array's length because there is a chance that the input array doesn't contain both of the input numbers whose distance we must find. In other words, if the input array doesn't contain any of the two input numbers, nDis will equal the array's length at the end of the method. Moreover, we must also initialize nDis to a large number that is not obtainable by any pair of numbers in the array because we are trying to find the minimum distance. If we initialize nDis to 0, it's more complicated to use nDis to keep track of the minimum distance. nDis = 0 is already the smallest possible distance between any two elements in an array.
3. The for loop will go through the entire input array ,nInputArray once. At each iteration, we do the following:
   • If the current element, nInputArray[i], equals to the first input number, nNum1, then assign nPos1 to that element's index, i. On the other hand, if the current element's value equals nNum2, then assign nPos2 to that element's index. Otherwise, we do nothing.
   • Next, we check if both of the index trackers' values have changed. If the values of nPos1 and nPos2 are less than the input array's length, it means that nNum1 and nNum2 exist in the input array. Again, we are guarding against the possibility that nNum1 or nNum2 is not in the input array.
   • If nPos1 and nPos2 are less than their initial values, then both nNum1 and nNum2 are present in nInputArray. Thus, we need to find out whether the new distance between nNum1 and nNum2 is less than the current minimum distance, nDis. If the new distance is less than nDis, we change nDis to the new distance. Note that we use the absolute value of the difference between nPos1 and nPos2 to figure out the distance. The reason are that nPos2 may be smaller than nPos1 and that we don't care about the numbers' order.
4. After the for loop, we check to see whether nDis is different from its initial value which is the input array's length. If nDis equals its initial value, input numbers are not present in the input array. We return -1 as an error indicator. However, if nDis is different from its initial value, both input numbers must be in the input array. Therefore, we return nDis as the minimum distance between those two numbers.

I hope the code and the explanation are clear. However, if you have any question, please let me know by emailing or commenting. Thanks for reading :)

Convert Binary Tree to Double Linked List in Zig-Zag Order

Question: given a binary tree, write an algorithm to convert the tree into a double-linked list. The list must be as if the tree is traversed in zig-zag and level order.

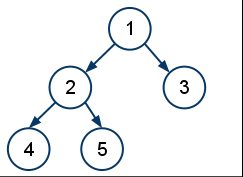
Solution: let's first understand what the objective is. By zig-zag level order, the question means that we need to traverse the tree in level order, a.k.a breadth first, such that the next level is traversed in the oposite direction to the current level. For example, take a look at this tree:

A zig-zag level-order traversal creates the list 1, 2, 3, 5, 4. It doesn't matter which direction the root is printed because there is only one node. However, since the second level is printed left to right, 2 then 3, the third level is printed from right to left, 5 then 4.

Now we understand the question, let's figure out how to solve this problem. Well, the only tricky part is to traverse the tree in zig-zag order. The other part, adding nodes to a linked list, is easy.

To solve this problem, we need two stacks. One stack stores nodes of levels that traversed from left to right. The other stores nodes of levels that traversed from right to left. The idea is to add the children of each node of the same level into a different stack than their parent. Thus, all children of the same level are in the same stack, separating one level from another. These children nodes are also pushed in the stack in the same direction with each other but opposite direction with their parents, so they can be traversed in the opposite direction to their parents. Moreover, as we traverse the tree, we add each node into a double linked list. Here is the implementation in C++:

struct Node* bt2ZigZagDoubleLinkedList(struct Node* root)
{
  if (root == NULL)
    return NULL;

  struct Node* head = root;
  struct Node* listIT = NULL;
  struct Node* prevNode = NULL;
  
  stack left2RightStack;
  stack right2LeftStack;

  left2RightStack.push(root);
  
  while (!left2RightStack.empty())
  {
    //add nodes from left to right to the list
    while (!left2RightStack.empty())
    {
      //set previous node
      prevNode = listIT;
    
      //pop a node in left2RightStack and add it to list
      listIT = left2RightStack.top(); 
      left2RightStack.pop();

      //add child nodes of the newly node in right to left direction
      if (listIT->left != NULL)
        right2LeftStack.push(listIT->left);
      
      if (listIT->right != NULL)
        right2LeftStack.push(listIT->right);

      //set left pointer of current node to the node in front of it
      listIT->left = prevNode; 

      //the previous node points to the current node in list
      if (prevNode != NULL)
        prevNode->right = listIT;
    }

    //add nodes from right to left to the list
    while (!right2LeftStack.empty())
    {
      prevNode = listIT;
      
      listIT = right2LeftStack.top();

      right2LeftStack.pop();

      if(listIT->right != NULL)
        left2RightStack.push(listIT->right);
        
      if(listIT->left != NULL)
        left2RightStack.push(listIT->left);

      listIT->left = prevNode;

      if (prevNode != NULL)
        prevNode->right = listIT;
    }
  }

  //connect linked the end node of list to NULL and the node in front of it
  listIT->right = NULL;
  listIT->left = prevNode;
  
  return head;
}

Code explanation: the method accepts the tree's root node as its parameter and return the head node to the double linked list.

1. First two lines check for null node, empty tree. If the tree is empty, we return an empty linked list.
2. The next three lines declare three pointers to tree nodes. head points to the head node of the linked list. We initialize it to the root node because the root node will be the first node in the list. listIT will be the iterator to traverse the tree. prevNode points to the last node visited by listIT. We need it to construct the double linked list since we must point the previous node to the current node and the current node back to previous node.
3. We also create two stacks that contain pointers to tree nodes. left2RightStack contains nodes in left to right order while right2LeftStack contains nodes in right to left order.
4. We then initialize left2RightStack by pushing the root node inside it.
5. There are three different while loops. The first while loop makes sure that we visit all nodes in the tree and add them into our double linked list. The two inner while loops make sure that we add the nodes level by level and in opposite directions. We do the following in the first inner while loop:
   • First, we pop a node off the left2RightStack and assign it to listIT.
   • Then, we add listIT's left child into the right2LeftStack before adding listIT's right child into the same stack. This guarantees that when we pop those children off the right2LeftStack they will be poped in the opposite order to their parent.
   • After that, we add listIT into the linked list. Pointing its left pointer to the node before it, prevNode
   • Finally, we point the right pointer of the prevNode to listIT. Remember we're making a double linked list, that's why we need to point the node in front of listIT, which is prevNode, to listIT.
   • The while loop runs until there is no nodes left in left2RightStack.
6. After the first inner loop traverses a level from left to right, the second inner while loop traverses the next level from right to left. The process is similar to that of left-to-right traversal. The only difference is that we add right children to the stack before left children.
7. Once all nodes have been added into the double linked list, we'll connect the end node of the list to the node before it and to a null node as the node after it.
8. Lastly, we return head. In the beginning, we have already assigned head to the root node which is the first node of the list, so head is point at the first node in the list.

That's all for this problem. If you find any mistake or have better solution, please feel free to let me know. Thanks for reading :)